Scientific article

GENETIC PARAMETERS FOR GROWTH AND REPRODUCTIVE TRAITS OF BROWN SWISS CATTLE FROM MEXICO

Parámetros genéticos para caracteres de crecimiento y reproductivos del ganado pardo suizo europeo de México

Ricardo del Carmen Chin-Colli¹, Raciel Estrada-León², Juan Magaña-Monforte¹*, José Segura-Correa¹, Rafael Núñez-Domínguez³

¹ Campus de Ciencias Biológicas y Agropecuarias, Facultad de Medicina Veterinaria y Zootecnia, Universidad Autónoma de Yucatán. Km 15.5 Carretera Mérida-Xmatkuil, AP 4-116, Mérida, Yucatán, México.

² InstitutoTecnológico Superior de Calkiní en el Estado de Campeche. Av. Ah Canul s/n por Carretera Federal. CP. 24900, Calkiní, Campeche.

³ Departamento de Zootecnia, Posgrado en Producción Animal, Universidad Autónoma Chapingo, Carretera México-Texcoco Km 38.5; CP. 56230, Chapingo, Estado de México

*Autor de correspondencia: jmagana@correo.uady.mx

Article received june 23, 2014
Accepted january 20, 2015

ABSTRACT

The aim of this study was to estimate the components of (co)variance and genetic parameters for birth weight (BW, n = 16 806), weaning weight adjusted to 240 d of age (WW240, n = 9 Oil), yearling weight (YW, n = 6 516), age at first calving (AFC, n = 5 974) and calving interval (Cl, n = 8 873) of Brown Swiss cattle from Mexico. Retrospective data from 1982 to 2010 were used from 86 ranches, spread across the country, which belonged to the Mexican Association of Registered Brown Swiss Cattle Breeders. Two trivariate analyzes were used considering BW-WW240-YW and YW-AFC-CI traits. The animal model included the contemporary group, direct additive, maternal additive, permanent environmental effects and the error term, plus age of cow at calving, parity and purebred degree as covariates. In general, direct heritabilities ranged from 0.03 to 0.35 and maternal heritabilities from 0.02 to 0.10. Correlations between direct and maternal additive genetic effects for BW, WW240 and YW ranged from -0.29 to -0.70. The direct genetic correlations for BW-WW240, BW-YW and WW240-YW were 0.51, 0.44 and 0.84, respectively, whereas for YW-AFC, YW-CI and AFC-CI they were -0.34, 0.14 and -0.26, respectively. In conclusion, selection for yearling weight could reduce the age at first calving without altering the calving interval.

Key words: Brown Swiss, heritability, genetic correlation

RESUMEN

El objetivo del presente estudio fue estimar los componentes de (co)varianza y parámetros genéticos para peso al nacimiento (PN, n = 16,806), peso al destete ajustado a 240 d de edad (PD240, n = 9,011), peso al año (PA, n = 6,516), edad al primer parto (EPP, n = 5,974) e intervalo entre partos (IP, n = 8,873) de ganado Suizo Europeo en México. Se utilizaron datos retrospectivos de 1982 a 2010, correspondientes a 86 ranchos distribuidos en todo el país, los cuales estaban registrados en la Asociación Mexicana de Criadores de Ganado Suizo de Registro. Se utilizaron dos análisis trivariados considerando las características PN - PD240-PA y PA - EPP - IP. El modelo animal incluyó los efectos de grupo contemporáneo, aditivo directo, aditivo materno, ambiental permanente y el error; además de las covariables edad de la vaca al parto, número de parto y grado de encaste. En general, las heredabilidades directas variaron de 0.03 a 0.35 y las maternas de 0.02 a 0.10. Las correlaciones entre los efectos genéticos aditivos directos y maternos para PN, PD240 y PA variaron de -0.29 a -0.70. Las correlaciones genéticas directas para PN-PD240, PN-PA y PD240-PA fueron de 0.51, 0.44 y 0.84, respectivamente; y para PA-EPP, PA-IP y EPP-IP fueron -0.34, 0.14 y -0.26. En conclusión, la selección por peso al año reduciría la edad al primer parto sin modificar el intervalo entre partos. Palabras clave: Suizo Europeo, heredabilidad, correlación genética.

Palabras clave: Suizo Pardo, heredabilidad, correlaciones genéticas

INTRODUCTION

Beef cattle production is one of the most important livestock activities in Mexico. In arid areas, Bos taurus breeds are preferred and in the central and southern areas both B. taurus and Bos indi-cus cattle breeds are used. Among the B. taurus breeds, Brown Swiss cattle are widely distributed as pure or crossbreed (Pell et ai 2010). In recent years, many efforts have been made to improve environmental conditions to increase beef production (Zorrilla-Rios et ai. 2013). However, another alternative to increase cattle production is through the genetic selection of the best animals (Montaldo and Barría 1998).

Growth and reproduction are relevant economical traits that should be included in a sound breeding program. Therefore, the knowledge of the genetic parameters and the relationship between them are required before a selection program could be implemented (Falconer y Mackay 1996). Estimation of genetic parameters has been performed basically on pre-weaning growth traits, in several European breeds (Ríos-Utrera 2008, Torres-Vázquez et ai. 2012). For Brown Swiss cattle, Segura-Correa et ai. (2012) reported pre-weaning growth and age at first calving genetic parameters in the tropics of Mexico and Estrada-León et ai. (2008) and Ríos-Utrera et ai. (2010) reported the heritabilities for some reproductive traits in a herd managed under the tropical conditions of Mexico.

Although the genetic evaluation of Brows Swiss cattle in Mexico started in 2003 (Núñez et ai. 2003), it has been focused on pre-weaning traits; therefore the amount of additive genetic variation of cow reproductive traits and their genetic relationship with growth traits is unknown. Age at first calving and calving interval are reproductive traits used as criteria for reproductive efficiency in all production systems and it could have a relevant impact on beef production cost, due to the impact on the cost of replacement heifers and the reduction in open days in cows. Meyer (2004) reported that cows with fast growing rates and high adult body weight tend to have poor reproductive performance, due to the genetic antagonism between those traits.

In Mexico, there is a lack of information on genetic parameter estimates on growth and reproductive traits for the Brown Swiss cattle breed, using multivariate models (Estrada-Leôn et ai. 2008, Segura-Correa et ai. 2012). The objectives of this study were to estimate covariance and variance components and genetic parameters (heritability and genetic correlations) for growth traits (birth, weaning and yearling weights) and for yearling weight, age at first calving and calving interval.

MATERIALS AND METHODS

Origen, animal management and data structure

Records on 128 447 European Brown Swiss animals, born between 1982 and 2010, from 86 farms located in the tropics of Mexico were used. All the herds were registered in the breeding program of the Mexican Brown Swiss Cattle Breeders Association. The association registers animals at least 31/32 Brown Swiss.

Calves were weaned at approximately 8 months of age, and they were reared under grazing condition with minerals or commercial feed supplementation. Reproduction occurred throughout the year, based mainly on artificial insemination and controlled natural mating. Additional information on animal feed and reproductive management is given by Ruiz-Flores et ai. (2006) and Ramirez-Valverde et ai. (2007).

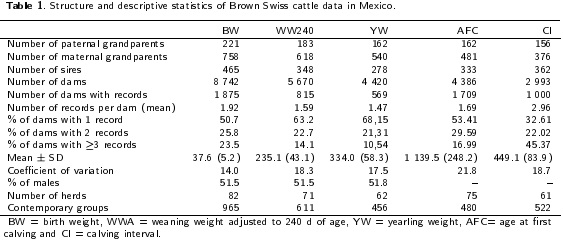
The traits used in this study were birth weight (BW, n=16 806), weaning weight adjusted to 240 d (WW240, n = 9 Oil), weight adjusted to a year of age (YW, n = 6 516), age at first calving (AFC, n = 5 974) and calving interval (Cl, n = 3 914). Descriptive statistics and structure of the data used here is shown in Table 1. According to Maniatis and Pollott (2003), the data had an appropriate structure for partition of the variation in co and variance components, like direct additive, maternal additive and environmental permanent effects; nearly 10 % of the data had dams with records as calves, more than 1.5 calves per cow and more than seven calves per bull.

Statistical Analysis

To define the fixed effects to be used in the mixed models analysis, least-squares analyses were performed by the MIXED procedure of the SAS program (SAS 9.0^®, SAS Institute, Cary, NC, USA). For each trait (BW, WW240, YW, AFC, Cl), the assumptions for an analysis of variance were tested. Records with ± 3.5 standard deviations from the mean were deleted. The linear model for growth and reproductive traits included the fixed effects of contemporary group (GC) and the age of dam as covariate (linear and quadratic). GC were integrated by herd (81), year of birth or calving (1982 to 2010), season of birth or calving (rainy and dry) and sex of calf (female or male; only for growth traits). GG had at least seven records (Ramirez-Valverde et al. 2008). Connectedness of CG was evaluated using AMC program (Roso and Schenkel 2006).

Estimation of genetic parameters

Components of co variance, variance and genetic parameters were estimated using restricted maximum likelihood (REML) method, fitting two tri-variate animal models (BW-WW240, YW and YW-AFC-CI) using the MTDFREML software package (Boldman et al. 1995).

The general animal model included contemporary group as fixed effect, the age of dam as a covariate, direct additive (d) and maternal additive (m) genetic effects, permanent environmental effect (pe) and the residual term (e), with covariance of d and m = 0, as suggested by Albuquerque and Meer (2001). In matrix notation the general animal model was:

y = Xβ + Z₁d + Z₂m + Z₃pe + e

Where: y = vector of observations; β= vector of fixed effects associated with the incidence matrix X; d = vector of direct additive genetic effects associated with the incidence matrix Z₁; m = vector of maternal additive genetic effects associated with the incidence matrix Z₂; pe = vector of permanent environmental effect associated with the incidence matrix Z₃; and e = vector of residual effects.

The general model was fitted for the first tri-variate animal model for growth traits (BW-WW240-YW), excluding permanent environmental effect for YW, according to the likelihood ratio test previously performed.

The assumptions relating to distribution of y, d, m, pe and e were:

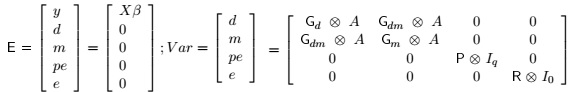
Where: G_d = 3x3 co variance matrix of direct additive genetic effects; G_m3x3 co variance matrix of maternal additive genetic effects; G^dm = G^md = 3x3 co variance matrix of direct additive-maternal genetic effects; P= 3x3 co variance matrix of permanent environmental effects; R= 3x3 co variance matrix of residual effects; A= Numerator relationship matrix; l_q = Identity matrix whose order is equal to number of dams; l₀ = Identity matrix whose order is equal to number of individuals with observations; = Kronecker operator (direct product between matrices). It is assumed that maternal additive genetic effects and permanent environment effects were not correlated. The convergent criterion used, was the variance of the values in the likelihood function (-2log L), considered to be smaller than 10^-6.

The second tri-variate animal model fitted (YW-AFC-CI), included the direct additive (d) and maternal additive (m) genetic effects, with covariance of a and m ≠ 0 for YW, direct additive (d) genetic effect for AFC and direct additive (d) genetic effect and the environmental permanent effect (ep) for Cl.

RESULTS

The values of the variance components, direct and maternal heritability estimates for BW, WW40 and YW are shown in Table 2. The correlations between direct and maternal genetic effects estimated in this study were negative and unfavorable (Table 3). Genetic and phenotypic correlations between BW, WW240 and YW are presented in Table 3. Genetic correlations between growth traits were positive and ranged from 0.44 to 0.84. The highest direct genetic correlation (0.84) was found between adjacent weights (WW240d and YW).

The results of the variance components, direct and maternal YW, AFC and Cl heritabilities are shown in Table 4. The direct heritabilities for YW, AFC and Cl were 0.35, 0.11 and 0.03, respectively. Maternal heritability for YW was 0.10. Table 5 shows the results of genetic and phenotypic correlations for YW, AFC and Cl. Direct genetic correlations were negative for YW and AFC (-0.34) and between AFC and Cl (-0.26) and positive for YW and Cl (0.14).

DISCUSSION

The direct heritability for BW (0.19) is lower than the direct heritability (0.37) reported by Ríos-Utrera (2008) but it is within the range of estimates reviewed, without including Brown Swiss populations. Sahin et al. (2012), Tulki et al. (2008) and Kaygisiz et al. (2011) reported lower direct heritabilities for Brown Swiss populations in Turkey and in Pakistan, respectively.

The direct heritability for WW240 (0.27) is within the range of values reported by Ríos-Utrera (2008). The direct heritability (0.35) for YW was similar to the results published by different authors (Cucco et al. 2009, Costa et al. 2011). Maternal heritabilities were low (0.02 to 0.07), indicating this the little importance of the maternal effects for the three growth traits. These results are within the range of estimates reported in the literature for weaning traits (Ríos-Utrera 2008). The importance of maternal effects at different ages, has been documented (Robinson 1996a, b, Meyer 1997), with production of milk and the care of the cow’s care of the calf (maternal ability) being the main effects (Meyer et al. 1994). Although the results revealed that estimates of direct heritability, for the three growth traits, were higher than the estimates of maternal heritability, the latter cannot be ignored in multitrait genetic evaluations.

In general, the heritability estimates for the three traits were moderate; therefore, the inclusion of these traits is justified in a screening program for improving the production of the Brown Swiss breed in Mexico, and hopefully the genetic selection for any of these traits will result in a future improvement. The negative and unfavorable correlations between direct and maternal genetic effects (Table 3), should be of great interest to breeders, because the maternal effect on the phenotype of the progeny of cows selected, may negatively affect the genetic progress for weaning weight by up to 20 % or more (Robison 1981).

Negative genetic correlations between direct and maternal genetic effects are commonly encountered in the literature in beef cattle (Koots et ai 1994b, Meyer 1997, Eriksson et al. 2004). Beker (1980) suggested that high and negative genetic correlations between direct and maternal additive effects may be a consequence of the negative correlation between the cow and the calf, probably due to an adverse effect of the high nutrition during the rearing of heifers on weaning weight of the offspring.

Robinson (1996b) mentioned that the structure of the analyzed data could cause an important bias, as well as additional variation due to sire and sire x year interaction or negative covariance between mother-offspring, which is a real genetic antagonism between traits. However, in this study the bias that the structure of the data could produce is expected to be minimal, due to the adjustment made. In the analysis of the data at least seven animals per contemporary group and a minimum of five offspring per sire were considered. In addition, all possible effects were considered in the final statistical model for the estimation of genetic parameters, based on the criterion of the likelihood ratio test. The high and negative correlations between direct and maternal additive genetic effects for the three characteristics indicate an unfavorable synergy. Therefore, selection for direct additive genetic effects is expected to reduce maternal ability.

The highest direct genetic correlation (0.84) found between adjacent weights (WW240d and YW, Table 3) suggests the presence of common genes that influence the three variables. Therefore, the selection of animals with high BW will increase WW240 and YW, and vice versa. But must be kept in mind that selection of animals with high PD240 or YW will increase the PN, which is not always desirable, as it can increase the frequency of calving difficulties (Zaborski et al. 2009), mainly in first calving cows. Unfavorable positive correlations between BW and the other two traits and positive correlation between WW240d and YW should be considered in selection programs for growth. Therefore, it is probably more effective to consider the BW and one of the other two traits in a selection index. In this sense, MacNeil (2003) evaluated the index, I = YW - BW 3.2, proposed by Dickerson et al. (1974), using a genetic correlation between BW and YW of 0.71, and they observed moderate genetic responses of 0.45, 3.42 and 7.74 kg^-1 generation at birth, at 200 d and at one year of age, respectively.

Regarding the heritabilities estimated for reproductive traits, generally in the literature they have low heritability (Koots et al. 1994a), except AFC. Roughsedge et al. (2005) and Estrada-León et al. (2008) reported values for AFC from 0.17 to 0.26 and 0.28, respectively. Therefore, it seems possible to improve the AFC through selection. However, Koots et al. (1994a) reported a heritability average of 0.06 for the AFC and Roughsedge et al. (2005) found a value of 0.05 for South Devon cattle, suggesting that in some breeds, this feature is strongly influenced by environmental factors. In this study, taking into account the heritability estimated (0.11), the improvement of the AFC would have better results if better management practices were implemented.

For Cl, the heritability (0.03) estimated in this study is very low but similar to the estimates from other studies. Based on three estimates, Koots et al. (1994a) reported a mean heritability of 0.10 for Cl. Roughsedge et al. (2005) estimated values ranging from 0.04 to 0.13 for four breeds of beef cattle and Estrada-León et al. (2008) found a value of 0.11 in a herd of Brown Swiss cattle in the tropics of Mexico. The results, in this study, indicate that the improvement of Cl had to be through better and sound management practices.

The negative but favorable correlation (Table 5) between YW-AFC and positive between YW-CI indicates that the heaviest females at one year of age will have their first calving at an early age but the Cl will increase. As a result, the selection based on YW may result in a reduction in the AFC but in longer calving intervals. Therefore, in the long term, this selection can increase mature weight (Grossi et al. 2008, Costa et al. 2011), which in a pasture based production system is undesirable and will also likely increase calving difficulty (Núñez-Domínguez et al. 1991, Martin et al. 1992). The moderate association between AFC and YW shows the importance of body weight of the heifer to the start of the reproductive life. Part of the genetic variation of AFC may be due to the variation in body weight (Nunez-Dominguez etal. 1991, Martin etal. 1992). However, the response to selection would be low, reducing AFC when only YW is considered in a breeding program. Thus, the inclusion of AFC in a selection index could improve sexual precocity of females (Roughsedge et al. 2005). Genetic correlations between weights at different ages and reproductive traits have been reported by several authors. A study reported genetic correlations between -0.06 to -0.18 for three breeds, indicating that selection for weight at 400 d of age results in a low AFC (Roughsedge et al. 2005). This result is similar to the correlation of -0.11 between YW and age at puberty reported by Gregory et al. (1995).

The estimated direct genetic correlation between YW and Cl was positive and unfavorable, indicating that selection for YW would increase Cl. Genetic correlations between weights at different ages and reproductive traits were estimated by Gutiérrez et al. (2007), indicating a negative association (-0.14) but positive between YW and Cl, which disagrees with what was found in this study. The age at first mating and consequently the AFC is more a function of body weight and the age of the animal; therefore, the common practice, in many herds, of adopting the minimum weight for mating heifers may cause the favorable relationship between the YW and AFC (Mercadante et al. 2003). As a result, high AFC is caused, in part by low growth rates due to poor nutritional status of replacement heifers (Renquist et al. 2006). In contrast, the unfavorable relationship between YW and Cl, is largely due to the fact that Cl is mainly affected by age, regardless of body weight, because cows with AFC at two years of age have longer Cl compared with cows calving for the first time at three years of age. After three years of age, there is little difference between the intervals of two subsequent calvings. The long first Cl is probably due to dystocia problems and delayed uterine involution associated with the age at first calving (Renquist et al. 2006). In addition, the poor performance of first calving cows is, partly because they are still growing and the demand for milk from the offspring subjected them to stress, causing a delay in ovarian activity.

CONCLUSIONS

The results indicate that selection for growth traits can result in joint and several favorable responses because of moderate heritabilities and positive association between them; however, the unfavorable genetic correlation between direct and maternal additive genetic effects must be taken into account. Selection for YW may have moderate positive effects on AFC. Correlation information may be required in the assessment of multi-trait reproductive variables to assist in the selection of bulls to produce replacement heifers for the herds.

LITERATURE CITED

Albuquerque LG, Meyer K (2001) Estimates of covariance functions for growth from birth to 630 days of age in Nelore cattle. Journal of Animal Science 79: 2776-2789.

Beker RL (1980) The role of maternal effects on the efficiency of selection in beef cattle - a review. Proceedings of New Zealand Society of Animal Production 40: 285-303.

Boldman KG, Kriese LA, Van Vleck LD, Van Tassel CP, Kachman SD (1995) A manual for use of MTD-FREML. A set of programs to obtain estimates of variances and covariances (DRAFT). U.S. Department of Agriculture, Agriculture Research Service, Lincoln, NE. 120p.

Costa RB, Misztal I, Elzo MA (2011) Estimation of genetic parameters for mature weight in Angus cattle. Journal of Animal Science 89: 2680-2686.

Cucco DC, Ferraz JBS, Pinto LFB, Eler JP, Balieiro JCC, Mattos EC (2009) Genetic parameters for preweaning traits in Braunvieh cattle. Genetics and Molecular Research 8: 291-298.

Dickerson GE, Kiinzi N, Cundiff LV, Koch RM, Arthaud VH, Gregory KE (1974) Selection criteria for efficient beef production. Journal of Animal Science 39: 659-673.

Eriksson S, Nasholm A, Johansson K, Philipsson J (2004) Genetic parameters for calving difficulty, stillbirth, and birth weight for Hereford and Charoláis at first and later parities. Journal of Animal Science 82: 375-383.

Estrada-León RJ, Magaña-Monforte JG, Segura-Correa JC (2008) Genetic parameters for reproductive traits of Brown Swiss cows in the tropics of Mexico. Journal of Animal and Veterinary Advances 72: 124-129.

Falconer DS, Mackay TFC (1996) Introducción a la Genética Cuantitativa. 4 edición. Editorial Acribia. Zaragoza, España. 469p.

Gregory KE, Cundiff JV, Koch RM (1995) Genetic and phenotypic (co)variance for growth and carcass traits of purebred and composite populations of beef cattle. Journal of Animal Science 73: 1920-1926.

Grossi DA, Frizzas OG, Paz CCP, Bezerra LAF, Lôbo RB, Oliveira JA,et a/ (2008) Genetics association between acummulated productivity, and reproductive and growth traits in Nelore cattle. Livestock Science 117: 139-146.

Gutiérrez JP, Goyache F, Fernández I, Alvarez I, Royo LJ (2007) Genetic relationships among calving ease, calving interval, birth weight, and weaning weight in the Asturiana de los Valles beef cattle breed. Journal of Animal Science 85: 69-75.

Kaygisiz A, Bakir G, Yilmaz I, Vanli Y (2011) Estimation of variance components and genetic parameters for direct and maternal effects on birth weight in Brown Swiss cattle. Pakistan Veterinary Journal 31: 70-74.

Koots KR, Gibson JP, Smith C, Wilton JW (1994a) Analysis of published genetic parameter estimates for beef production traits. 1. Heritability. Animal Breeding Abstracts 62: 309-338.

Koots KR, Gibson JP, Smith C, Wilton JW (1994b) Analysis of published genetic parameter estimates for beef production traits. 2. Phenotypic and genetic correlations. Animal Breeding Abstracts 62: 825-833.

MacNeil MD (2003) Genetic evaluation of an index of birth weight and yearling weight to improve efficiency of beef production. Journal of Animal Science 81: 2425-2433.

Maniatis, N, Pollott GE (2003) The impact of data structure on genetic (co) variance components of early growth in sheep, estimated using an animal model with maternal effects. Journal of Animal Science 81: 101-108.

Martin LC, Brinks JS, Bourdon RM, Cundiff LV (1992) Genetic effects on beef heifer puberty and subsequent reproduction. Journal of Animal Science 70: 4006-4017.

Mercadante MEZ, Packer IU, Razook AG, Cyrillo JNSG, Figueiredo LA (2003) Direct and correlated response to selection for yearling weight on reproductive performance of Nelore cows. Journal of Animal Science 81: 376-384.

Meyer K (1997) Estimates of genetic parameters for weaning environmental covariances. Livestock Production Science 52: 187-199.

Meyer K (2004) Estimates of covariance functions for growth of Angus cattle. Journal of Animal Breeding and Genetics 122: 73-85.

Meyer K, Carrick MJ, Donnelly BJ (1994) Genetic parameters for milk production of Australian beef cows and weaning weight of their calves. Journal of Animal Science 72: 1155-1165.

Montaldo VHH, Barría PN (1998) Mejoramiento genético de animales. Revista Ciencia al Día 1: 1-19.

Núñez, DR, Ramírez, VR, Ruiz, FA (2003) Resumen de evaluaciones genéticas para sementales Suizo Europeo 2003. Boletín Técnico. Departamento de Zootecnia. Universidad Autónoma Chapingo. Chapingo, México. 40p.

Nuñez-Dominguez R, Cundiff LV, Dickerson GE, Gregory KE, Koch RM (1991) Lifetime production of beef heifers calving first at two vs three years of age. Journal of Animal Science 69: 3467-3479.

Pell D, Jhonson RJ, Matheus KH (2010) Cow-calf beef production in Mexico. A report from the Economic Research Service, USDA. LPD-M-196-01. November 2010. Washinton DC. 24p.

Ramírez-Valverde R, Hernández-Álvarez O, Núñez-Domínguez R, Ruíz-Flores A, García-Muñiz J (2007) Análisis univariado vs multivariado en la evaluación genética de variables de crecimiento en dos razas bovinas. Agrociencia 41: 271-282.

Ramírez-Valverde R, Núñez-Domínguez R, Ruíz-Flores A, García-Muñiza JG, Magaña-Valencia F (2008) Comparación de definiciones de grupos contemporáneos en la evaluación genética de bovinos Suizo Europeo. Técnica Pecuaria en México 46: 359-370.

Renquist J, Oltjen J, Sainz R, Calvert C (2006) Effect of age on body condition and production parameters of multiparous beef cows. Journal of Animal Science 84: 1890-1895.

Ríos-Utrera A (2008) Estimadores de parámetros genéticos para características de crecimiento predestete de bovinos. Revisión. Técnica Pecuaria en México 46: 37-67.

Ríos-Utrera A, Calderón RRC, Rósete FJV, Lagunes LJ (2010) Estimación de parámetros genéticos para características de fertilidad en ganado Suizo Pardo bajo condiciones subtropicales en México. Veterinaria México 41: 117-129.

Robinson DL (1996a) Estimates and interpretation of direct and maternal genetic parameters for live weights of Australian Angus cattle. Livestock Production Science 45: 1-11.

Robinson DL (1996b) Models which might explain negative correlations between direct and maternal genetic effects. Livestock Production Science 45: 11-122.

Robison O (1981) The influence of maternal effects on the efficiency of selection; a review. Livestock Production Science 8: 121-137.

Roso VM, Schenkel RS (2006) AMC - A computer program to assess the degree of connectedness among contemporary groups. In: Proceedings of the 8th World Congress on Genetics Applied to Livestock Production. Belo Horizonte, Brazil, pp: 26-27

Roughsedge T, Amer PR, Thompson R, Simm G (2005) Genetic parameters for a maternal breeding goal in beef production. Journal of Animal Science 83: 2319-2329.

Ruíz-Flores A, Núñez-Domínguez R, Ramírez-Valverde R, Domínguez-Viveros J, Mendoza-Domínguez M, Martínez-Cuevas E (2006) Niveles y efectos de la consanguinidad en variables de crecimiento y reproductivas en bovinos Tropicarne y Suizo Europeo. Agrociencia 40: 289-301.

Sahin A, Ulutas Z, Yilmaz Adkinson A, Adkinson RW (2012) Estimates of phenotypic and genetic parameters for birth weight of Brown Swiss calves in Turkey using animal model. Tropical Animal Health and Production 44: 1027-1034.

Segura-Correa JC, Chin-Colli R, Magaña-Monforte JG, Núñez-Domínguez R (2012) Genetic parameters for birth weight, weaning weight and age at first calving in Brown Swiss cattle in Mexico. Tropical Animal Health Production 44: 337-341.

Torres-Vázquez JA, Manzanilla-Pech CIV, Borrayo-Cepada A, Ríos-Utrera A, Vega-Murillo VE, Martinez-Velázquez G,et a/. (2012) Genetic and phenotypic parameters for yearling weight, scrotal circumference and frame score in Simmental and Simbrah beef cattle from Mexico. Revista Mexicana de Ciencias Pecuarias 3: 291-298.

Tulki M, Saatci M, Colak M (2008) Genetic parameters for direct and maternal effects and estimation of breeding values for birth weight in Brown Swiss Cattle. Turkish Journal of Veterinary and Animal Sciences 32: 287-292.

Zaborski D, Grzesiak W, Szatkowska I, Dybus A, Muszynska M, Jedrejczak M (2009) Factors affecting dystocia in cattle. Reproduction in Domestic Animals 44: 540-551.

Zorri I la-Ríos JM, Lancaster PA, Goad CL, Horn GW, Hilton GG, Galindo JG (2013) Quality evaluation of beef carcasses produced under tropical condition of Mexico. Journal of Animal Science 91: 477-482.